Spending your way to success – an investor’s guide.

By ANDREW WATSON

How much do budgets really affect a league table?

Often we hear stakeholders in the game, be they fans, owners, managers, say things such as “On our budget we should…” or the famous “We have the smallest budget in the league.” This quote belonged to at least six Championship sides in 2021/22 according to the media.

Indeed, it is widely accepted that budget, transfer or wage, does have an impact on where a club can realistically expect to finish over the course of a season. The question is: How much of an impact does it have?

The Difficulties With Financial Data

Obviously this is a very difficult question to answer with any degree of certainty. 

The initial problem is that accurate financial data is difficult to come by, especially for all clubs in a league. Some may not enter accounts, if they do then they may not be full accounts. Even then the latest available accounts are often two years out of date.

The data used is therefore imperfect. but when comparing the accounts of clubs who do publish full breakdowns and other sources (wage estimates of individual players) we can accurately estimate which clubs are the highest and the lowest paying within any given league. 

Building A Probability Model

The next step is establishing a relationship between the financial data and the football.

In this example we have used data from English League One. Accessing data for the football teams in this league is straightforward because of the availability of historic goals, xG and points.

Data was gathered for seasons 2017/18 up to 2021/22. From this we were able to establish what relationship the wage budget had with the performance and results variables.

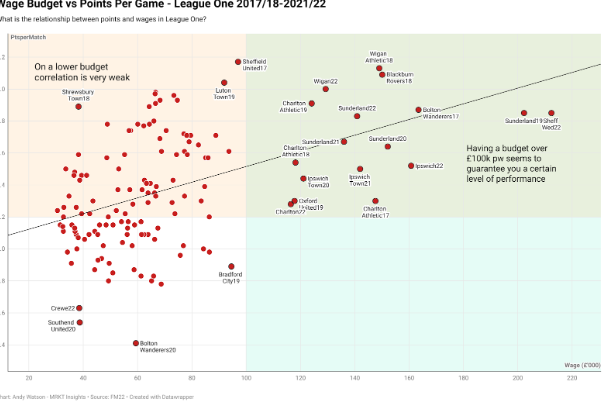
Also at this stage we could produce an initial graph that demonstrated the general relationship between points won and wage budget.

As we would expect there is indeed a positive correlation between wage budget and points won.

However, what is clear is that a low budget in League One could mean anything in terms of points won. Some low budget teams had exceptional seasons, such as Shrewsbury Town’s 2017/18 3rd place and Luton Town’s 2018/19 title winning years.

Equally, all of the desperately poor seasons in the last few years have come from clubs who are clearly struggling financially. 

On the graph it is possible to draw lines in to create a sector by which it is possible to identify the point at which a certain size of budget almost guarantees a degree of safety in League One, if not competitiveness. No club with a wage budget over £100k per week has won points at less than 1.2 points per game.

However, a big budget is no guarantee of success. Indeed the four biggest estimated budgets in the sample all failed to achieve promotion. The highest points per game ratio in the sample was achieved by Chris Wilder’ 2016/17 Sheffield United, which is estimated at just under £100k per week budget.

Calculating “best guess” probabilities

Now that the relationships have been established we can take the coefficient of determination for goals for, goals against, xG and xGA to help us simulate a full season of League One.

Taking Accrington as an example, their estimated budget is one of the lowest in the league. Therefore, as this model is solely concentrating on budget as the only variable of success, their performance and results should match up to around their budget stature.

To do this we took Accrington’s budget and found the difference between that and the average League One 22/23 budget. Earlier we had calculated the average xG per match in League One to be 1.41, with an 11% causation to budget. Therefore we can then use the difference in budget as a variable to find an xG value for a team with Accrington’s budget. In this case, 1.36xG per match.

We can do the same with xGA (1.49), goals scored (1.24) and goals conceded (1.4). At the end of this we are in a position to give Accrington a budget-based rating that will be used in the simulations. 

When Accrington play a match there will be a number of goals they will be expected to score and a number they expect to concede. Those two numbers are estimated from the calculations above where xG and goals scored are put into a 65:35 ratio (xG has a better predictive value) and xGA and goals conceded are used in the same way.

This gives Accrington final ratings of 1.32 goals and 1.46 against. This is just a base for the simulation to work with, but if a team ended up with these figures as an average for the season you may realistically expect a bottom half finish from this side.

Single Season Simulation

Once all the clubs are assigned goals for and against ratings then a fixture list is devised. The 24 teams all play each other twice to a total of 46 matches per club. In each of these matches a random number is assigned to each team based upon their respective ratings.

Just as in real football, this means that just because a team has a higher rating that the other doesn’t mean that they will automatically win that game. This is the element of randomness that we love about football, this time coded into the simulation via random numbers.

If the gap between the generated numbers in a fixture is greater than 0.35 either way then a win is awarded. Below 0.35 difference is classed as a draw. All 46 league games for Accrington were simulated and in the initial season they won 51 points. That was good enough for 15th place in this first season, with MK Dons surprisingly finishing rock bottom with 39 points. 

Also relegated were new boys Exeter City (23rd) and Forest Green Rovers (21st), with lowest budget Cambridge United in 22nd.

The league was won by Sheffield Wednesday on 85 points. Derby County bounced straight back to the Championship as well, with Charlton Athletic, Fleetwood Town, Ipswich Town, and Plymouth Argyle filling the playoff positions.

1000 Season Simulation

You may think that these results don’t seem realistic. However, the only way to prove that is to conduct a more thorough examination of the model.

We do this by running the simulation multiple times. The more times a simulation is run, the more reliable the data is, think that classic mathematics lesson of rolling a fair dice. Rolling it six times it would be very unlikely to get a 1,2,3,4,5,6 to show up in the first six rolls, despite the chances of each one being equal (⅙). However, if you were to roll it 6000 times, the probabilities of rolling each number will gradually even out to that ⅙ figure. 

Completing this simulation 1000 times gives us far more interesting and accurate results on where a League One team “should” finish if based on budget alone.

Unsurprisingly Sheffield Wednesday “should” be Champions. They have the biggest budget in the division, and indeed, our budget-only model has them being automatically promoted 95.5% of the time.

Ipswich’s chances of automatic promotion are over 50% as well, whilst Morecambe had one miracle season in 1000 where they made it to the Championship! Only Exeter, Cheltenham, Accrington and Cambridge never attain automatic promotion over the 1000 seasons. Every team makes the playoffs though.

Down at the other end, Cambridge’s chances of relegation in this model are 53.6%. So despite having the lowest estimated budget in the league their chances of going down are still only close to 50:50. Which, when you take into account Mark Bonner’s excellent job and the recruitment, makes sense as to how they were able to avoid relegation fairly easily last term.

How can MRKT Insights use this model?

It is all very well being able to map this out but is this information useful?

As always we need to consider context.

Why might it be that the largest budget teams who should be promoted miss out? These teams are often the relegated Championship teams. They will often be teams in financial trouble, they will be carrying contracts for players who simply are not worth the money they are being paid. Three players on £20k a week contracts may equal the total wage bill of a rival team. 

Starting with a blank slate we would expect the relationship between budget and finishing position to be much stronger. But teams don’t start with blank slates, you always inherit the legacy of decisions made by previous regimes.

Despite these obvious caveats we still find this to be useful information to communicate.

First of all, we can use this to set baselines of performance. Where should we finish given our budget.  This helps to set a realistic performance target but also focuses the mind on the processes that serve to beat the forecast i.e. quality recruitment, excellent coaching and shrewd tactical management. 

Another use is for current owners to understand what implications a change in budget may have. With the budget being the main variable in the model we are able to change it and map the difference in results. If we are looking for a return on investment what is the baseline we should looking at in points at the end of the season. If a £500k budget increase should see an additional 3 points we want to beat that return.

If a club was facing financial difficulties and had to reduce their budget, we are in a position to forecast how much risk was being taken on and how much could be cut to stave off relegation or to still have a good chance at the Top 6.

And, of course, this works brilliantly for potential investors who may be interested in entering the world of football club ownership. Often the key question we are asked is “How much would it cost to do x, y or z?” A model such as this, or more likely an adaptation of this, is able to break down these questions and contextualise our answers.

However, this is only a model. Real life, and football especially, are subject to variance. We calculated that in League One 22% of the points accrued can be attributed to the club’s budget. This is very different in other leagues, the correlation is much stronger in the Premier League for example. 

We therefore calculate the individual league correlations, this allows us to identify the leagues and teams within them we believe are best placed to able to be succeed in the near future, and the budgets that will be required to do this.